Ввод формул в ячейку начинается с ввода символа =, за которым следует выражение (арифметическое, логическое, текстовое). Выражение строится из констант, ссылок на ячейки и диапазоны ячеек, обращений к функциям, разделенных знаками операций (операторами) и круглыми скобками. Excel вычисляет выражение и отображает в ячейке результат вычисления. Возможность применять в вычисляемых формулах в качестве аргументов ссылок на ячейки (адресов) является одним из основных достоинств MS Excel. Если после завершения ввода формулы в какой-либо ячейке-аргументе изменится значение, то Excel сразу же автоматически пересчитает новый результат и заменит им прежнее значение в ячейке.
В выражениях в первую очередь вычисляются функции и части, заключенные в круглые скобки, а затем выполняются операции в порядке уменьшения их приоритетов.
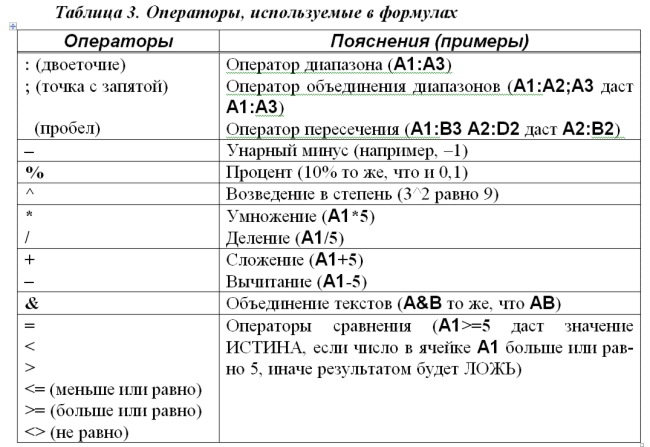
В приведенной ниже таблице представлены знаки операций, используемые в формулах.
Таблица 3. Операторы, используемые в формулах
Excel предоставляет большой набор различных встроенных функций, имеющих разные назначения. Назначение функции определяет ее категорию. Встроенные функции можно использовать в формулах для вычисления значений математических функций, обработки статистических и финансовых данных, преобразований текстов и другие.
Если Вам известно принятое в Excel имя функции и ее синтаксис (т.е. правила записи названия функции и ее аргументов), то ввести функцию и аргументы можно с клавиатуры. Однако Excel позволяет облегчить такой ввод и избежать ошибок, вызванных незнанием правил записи обращений к функциям, если воспользоваться Мастером функций.
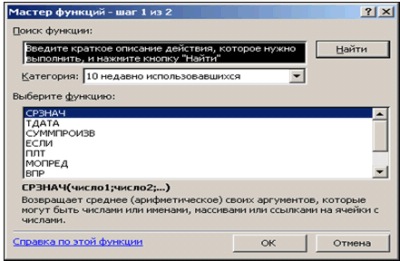
Ввод формул начинается с выделения ячейки, в которую и будет вставлена формула. При вводе простых формул (без обращения к Мастеру функций) сначала вводится знак =, который отобразится в активной ячейке (и в Строке формул). Одновременно в активной ячейке появится курсор, приглашающий вводить вычисляемое выражение. Чтобы воспользоваться для ввода формулы Мастером функций, достаточно щелкнуть в Строке формул по кнопке тогда одновременно с появлением в активной ячейке (и в Строке формул) знака = откроется диалоговое окно Мастера функций (рис. 26):
При этом в Строке формул появляется палитра формул: кнопка Отмена  , предназначенная для отмены ввода формулы или внесенных в нее изменений, и кнопка Ввод
, предназначенная для отмены ввода формулы или внесенных в нее изменений, и кнопка Ввод  , предназначенная для подтверждения введенной в ячейку формулы или результатов ее изменений, открывающийся список встроенных функций.
, предназначенная для подтверждения введенной в ячейку формулы или результатов ее изменений, открывающийся список встроенных функций.
В окне Мастера функций в раскрывающемся списке Категория: нужно выбрать соответствующую категорию функций, а затем из списка в окне Выберите функцию: – выбрать необходимую функцию.
Если аргументом функции является ссылка на ячейку или диапазон ячеек (возможно, на другом листе книги), то для ввода достаточно выделить соответствующую ячейку или диапазон ячеек. Чтобы при этом окно диалога не загораживало лист книги, его можно убрать, щелкнув по кнопке  справа от поля ввода, оставив видимой только эту строку. Для восстановления окна диалога после ввода аргумента нужно щелкнуть там же по кнопке
справа от поля ввода, оставив видимой только эту строку. Для восстановления окна диалога после ввода аргумента нужно щелкнуть там же по кнопке  . Аргументом функции может быть также выражение, в том числе обращение к функции или содержащее обращения к функциям. Для их ввода можно вновь воспользоваться Мастером функций.
. Аргументом функции может быть также выражение, в том числе обращение к функции или содержащее обращения к функциям. Для их ввода можно вновь воспользоваться Мастером функций.
В диалоговом окне Мастера функций имеется гипертекстовая ссылка Справка по этой функции для получения подробной информации о назначении и работе с выделенной функцией.
Особое место среди функций занимает функция СУММ, которую можно вызвать с помощью специальной кнопка Автосумма  При щелчке на ней сразу вставляется функция суммы для ближайшего диапазона заполненных ячеек в качестве аргумента. Аргумент можно скорректировать, выделив нужный диапазон ячеек.
При щелчке на ней сразу вставляется функция суммы для ближайшего диапазона заполненных ячеек в качестве аргумента. Аргумент можно скорректировать, выделив нужный диапазон ячеек.
В качестве примера использования функций рассмотрим формулы, вычисляющие корни квадратного трехчлена: ax2+bx+c=0. Они введены в ячейки A2 и A3 и имеют следующий вид:
=(-B1+КОРЕНЬ(B1*B1-4*A1*C1))/2/A1
=(-B1-КОРЕНЬ(B1*B1-4*A1*C1))/2/A1
В ячейках A1, B1 и C1 находятся значения коэффициентов a, b и с, соответственно. Если вы ввели значения коэффициентов a=1, b=-5 и с=6 (это означает, что в ячейках A1, B1 и C1 записаны числа 1, 5 и -6), то в ячейках A2 и A3, где записаны формулы, вы получите числа 2 и 3. Если вы измените число в ячейке A1 на -1, то в ячейках с формулами вы получите числа -6 и 1.
Коды ошибок
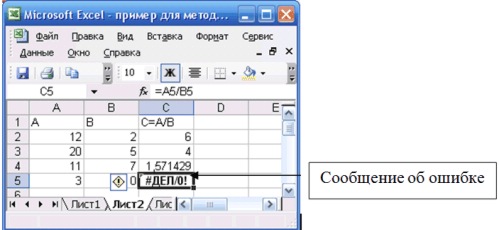
Если в ячейке невозможно вывести значение или вычислить результат формулы, Excel выводит на экран код ошибки (рис. 27). Выше приведен список кодов распространенных ошибок.
Таблица 4. Расшифровка кодов ошибок
#### - столбец слишком узок для отображения числа: либо расширьте столбец или уменьшите размер шрифта, либо измените формат числа.
#ДЕЛ/0! - деление на ноль является недопустимой операцией. Имейте в виду, что при выполнении операций над числовыми (текстовыми) данными ссылка на пустую ячейку будет представлять нулевое значение (пустую строку).
#Н/Д - данные “недоступны”, поскольку формула ссылается на недоступную функцию или значение.
#ИМЯ? - формула ссылается на неизвестное Excel имя.
#ЧИСЛО! - формула использует некорректное число. Например, в функции числовой аргумент не является числом.
#ССЫЛКА! - ссылка на ячейку больше недействительна: возможно, вы удалили ячейку или переместили на ее место другую.
#ЗНАЧ! - формула содержит некорректную операцию или аргумент: возможно, Вы пытаетесь сложить текстовое и числовое значения.
#ПУСТО! - задано пересечение двух областей, которые в действительности не имеют общих ячеек.
Дополнительные сведения по ошибкам можно получить непосредственно при возникновении ошибки, используя меню раскрывающегося списка, появляющегося рядом с ячейкой, или всплывающую подсказку на раскрывающемся списке.
Абсолютные, относительные и смешанные ссылки на ячейки
Ссылка есть указание в формуле адреса ячейки, содержимое которой должно быть использовано при вычислении формулы. Существуют три типа ссылок на ячейки: относительные, абсолютные и смешанные. Относительная ссылка - это ссылка, состоящая из имени столбца и имени строки, например, B5. Абсолютная ссылка - это ссылка, перед именами столбца и строки которой стоит символ $, например, $B$5. Имена ячеек и диапазонов в формулах также представляют абсолютные ссылки на них. Различие между относительной и абсолютной ссылками проявляется при копировании (распространении с помощью маркера заполнения) формулы в другую ячейку. В формуле-копии аргумент, заданный абсолютной ссылкой, не изменится, а у аргумента, заданного относительной ссылкой, номер строки (столбца) изменится на величину разности номеров строк (столбцов) ячеек, содержащих копию формулы и оригинал.
Например, если скопировать формулу =СУММ(A1:A3) из ячейки A4 в ячейку B5, то копия будет иметь вид =СУММ(B2:B4).
Допускаются и смешанные ссылки, когда одна из составляющих задана как абсолютная, со знаком $ (например, A$4 или $A4); она не изменяется при копировании и распространении формулы. Быстро заменить один из вариантов ссылки на любой другой (абсолютный, относительный, смешанный) можно последовательным нажатием клавиши F4, предварительно разместив рядом с ней в формуле курсор ввода.
При перемещении формулы в новое место таблицы ссылки в формуле не изменяются.